Since the beginning of the war in Ukraine and sanctions imposed by countries around the world on Russian, many have come to believe in the imminent default of Russia’s sovereign debts, which hasn’t happened in over a century. In this post, we will use survival analysis on credit default swaps to determine what the market participants believe is the probability that Russia will default on its sovereign debts.
Survival Analysis Concepts
Survival analysis originates in the analysis of clinical trials and deals with the survival function S(t), which is the probability that some defined event, such as death, doesn’t happen before time t. In our case, S(t) is defined as the probability that the Russia doesn’t default on its bonds before time t.
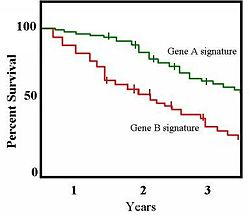
Survival curves observed in clinical experiments (source: https://en.wikipedia.org/wiki/Kaplan%E2%80%93Meier_estimator)
A concept central to survival analysis is the hazard rate, which is often used to model the survival function. Let T be the random variable for the time when a default happens, and f(t) is its probability density function. Hazard rate is defined as:
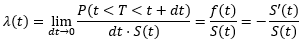
Intuitive, supposed a hazard rate λ is constant in a time interval between t1 and t2, then λ(t2 – t1) is the conditional probability that a default occurs between time t1 to t2 given no event occurred before t1. The survival function can be derived from the hazard rate and vice versa through the following relationship:
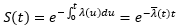
Define Q(t) as the probability that a default occurs by time t, we then have:
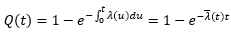
Credit Default Swap
Credit default swap (CDS) is a popular credit derivative used to hedge against default risk, which became especially prominent in the 2008 credit crisis. In a CDS transaction, a protection buyer agrees to pay a protection seller a spread on a notional principal amount of an underlying instruments issued by a reference entity over a period of time. In exchange, the protection seller will pay the buyer the loss on the principal amount of the underlying instrument in the event of a default. In our case, the underlying instrument is the Russian sovereign bonds, and the reference entity is the Russian government.
When a default happens, the CDS is now commonly settled in cash in which a IDSA-organized auction process is used to determine the cheapest to deliverable bond a few days after the credit event and the payoffs will be the difference between this bond the original face value. For example, if the auction judges the currently value of the bond to be $40 per $100 of face value, the cash payoff for the buyer will be $60. Hence, it’s important to specify a recovery rate R in the analysis of CDS (40% in the example above). A CDS variant called binary CDS pays out the full notional principal instead and its spread can be compared to the plain CDS to find the recovery rate. In addition, the buyers still need to pay an accrual on the CDS spread to the seller depending on when the default happens.
Various other instruments whose value involve credit risk factor can also be used for default probability analysis instead, such as asset swap, total return swap, collateralized debt obligation (CDO), synthetic CDO or simply bond yields spread. However, CDS is chosen in our case since it’s the most convenient for the case study here, has simple workings, is sufficiently liquid and the CDS spread directly reflects credit risk without depending on a certain risk free rate.
Risk Neutral Valuation Principle
When valuing derivative instruments, we work in a risk neutral world in which all market participants always expect the risk-free rate of returns. Intuitively, this is because derivatives are simply functions of some underlying risk variables (market risk, interest rate risk, exchange risk, credit risk) which already price in the fundamental sources of uncertainties, and hence the value of the derivatives themselves shouldn’t depend on the expected returns on those underlying instruments. Mathematically, the risk neural valuation emerges from the Black–Scholes–Merton differential equation that all derivatives satisfy in which the value of the derivatives do not depend on the rate of returns of the underlying stochastic variables.
In our case, if credit risk factor is removed, we won’t expect to earn any more than the risk-free rate on the derivative transaction on top of the underlying debts instruments. The default probability calculated in a risk neutral world is usually higher than the real-world default probability. This results in the excess returns earned, for example, by corporate bonds holders over government bonds, which could be explained as the returns required for taking systematic risks from default correlation or undiversifiable non-systematic risks due to the difficulties of hedging in the illiquid bonds market. Note that outside of derivatives valuation, such as scenarios analysis or VaR calculations, the real-world default probabilities as observed from historical data or Monte Carlo simulation should be used instead.
Implied Hazard Rate from CDS Spreads
We are now ready to compute the hazard rates, and hence the default probabilities, implied from the spread CDS buyers required to pay sellers for the reference Russian sovereign bonds. There are three separate components we need to formulate for this (from the perspective of the CDS buyer): the expected spread payments, the expected payoffs and the expected accruals.
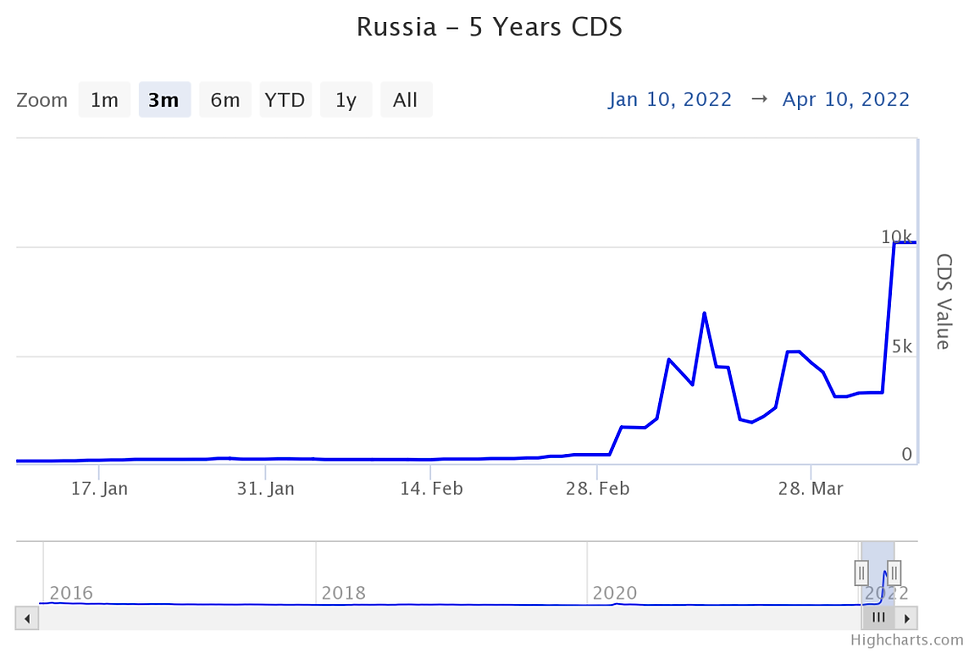
Historical CDS values (Data: http://www.worldgovernmentbonds.com/cds-historical-data/russia/5-years/)
Let s be the spread payment and ƛ be the average hazard rate on the 5 years CDS on Russian sovereign bonds. Suppose the payment is made semi-annually, the expected payment on each of the payment scheduled date for each $1 of principal is:
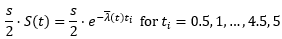
Discounting at risk free rate r, we have the present value of the expected CDS spreads payment per $1 of principal as:
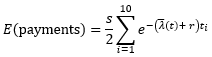
Russian sovereign bonds pay out its coupons semi-annually around mid-March and end of August. It has a 30 day grace period to meet this obligation before a default is declared. Hence, a possible default event would happen around April and September. Suppose it’s the beginning of this year, let τi = 0.25, 0.75, …, 4.25, 4.75 as the series of times to default.
Let R be the recovery rate on the underlying bonds, the expected payoffs per $1 of principal to a CDS buyer if a default occurred during a period from τi-1 to τi is:

Therefore, the present value of the expected payoffs per $1 of principal for the CDS buyer is:
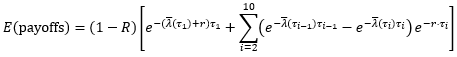
Since a default event may occur half-way between each spread payment date, a quarter of the annual spread s would need to be paid by the CDS buyer as accrual after the default event. The expected accrual when that happens during a period from τi-1 to τi is therefore:
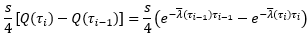
The present value of the expected accruals is then:
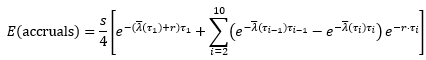
Since holding a bond and buying a corresponding CDS protection is approximately equivalent to converting a risky bond into a riskless bond (this is not entirely true in practice due to complications with the settlement process), in order for a arbitrage scenario not to happen (e.g. buying a risky bond and CDS while shorting a riskless government bond or vice versa), the present value of the expected payoffs should equal the present value of the total of expected spread payments and accruals. Therefore, the implied average hazard rate is one that satisfy the following equation:
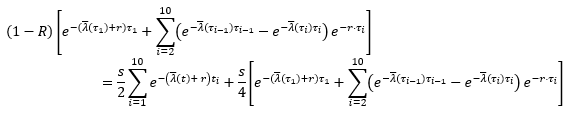
So, what’s the Russian sovereign bonds default probabilities?
On March 8th, 2022, the 5-year CDS spread on Russian sovereign bonds reach a record 4812 basis points for the first time (bps), essentially requiring CDS buyer to pay almost half of the principal amount to insure against default. Setting s = 48.12%, r = 3% (based on the SOFR benchmark) and R = 40%, a numerical solver returns a hazard rate of 37.96% per year that satisfies the above equation. This corresponds to a 85% probability of default within 5 years expected by the market.
After the US Treasury Department accepts an exception to allow coupon pay-out to US bank accounts for Russian sovereign bonds, narrowly escape the default on the March payment, the CDS spread drops to 2037 bps which implies a hazard rate of 16.52% per year and 56% probability of default within 5 years.
As of today, US Treasury Department again forbids coupon payments from being paid out by the Russian government to US bank accounts, essentially making a default inevitable. The CDS spread soars to 10207 bps which implies a hazard rate of 80.28% per year and a default probability of 98% within 5 years.

Comments